วิชา คณิตศาสตร์: บทที่2

ความน่าจะเป็นของเหตุการณ์ คือ จำนวนที่แสดงให้ทราบว่าเหตุการณ์ใดเหตุการณ์หนึ่ง มีโอกาสเกิดขึ้นมากหรือน้อยเพียงใด

เมื่อ P (E) คือ ความน่าจะเป็นของเหตุการณ์ E

n (E) คือ จำนวนผลที่จะเกิดขึ้นในเหตุการณ์ E

n ( S) คือ จำนวนผลทั้งหมดที่อาจจะเกิดขึ้นได้

จำนวนผลที่จะเกิดขึ้นในเหตุการณ์ E เรียกอีกอย่างหนึ่งว่า เหตุการณ์ที่สนใจ หรือสิ่งที่โจทย์กำหนดให้

จำนวนผลทั้งหมดที่อาจจะเกิดขึ้นได้ S เรียกอีกอย่างหนึ่งว่า แซมเปิลสเปซ หาได้จากการทดลองสุ่ม

ข้อสังเกต ถ้า E เป็นเหตุการณ์ใดๆ จะพบว่า

1) 0 < P(E) < 1

2) P(E) = 0 เมื่อ E เป็นเหตุการณ์ที่เป็นไปไม่ได้

3) P(E) = 1 เมื่อ E เป็นเหตุการณ์ที่แน่นอน

อธิบายความได้ว่า 1. ความน่าจะเป็นของเหตุการณ์ที่เป็นไปได้ เป็น 0

2. ความน่าจะเป็นของเหตุการณ์ใดๆจะเป็นจำนวนใดจำนวนหนึ่ง

ตั้งแต่ 0 ถึง 1

ผลทั้งหมดของเหตุการณ์หรือแซมเปิลสเปซ

แซมเปิลสเปซ(Sample Space) คือเซตของผลลัพธ์ที่อาจจะเกิดขึ้นได้ทั้งหมดจากการทดลองสุ่มและเป็นสิ่งที่เราสนใจ เรานิยมใช้สัญลักษณ์ S แทนแซมเปิลสเปซ จากความหมายของแซมเปิลสเปซ แสดงว่า ในการทดลองหรือการกระทำใด ๆ ก็ตาม ผลลัพธ์ที่มีโอกาสจะเกิดขึ้นได้ต้องเป็นสมาชิกในแซมเปิลสเปซทั้งสิ้น

ตัวอย่างที่ 1   การหาแซมเปิลสเปซในการโดยเหรียญ 1 เหรียญ ถ้าเราสนใจหน้าที่หงายขึ้น
                     ผลลัพธ์ที่อาจจะเกิดขึ้นได้คือ หัว หรือ ก้อย
                      ดังนั้น  แซมเปิลสเปซที่ได้ คือ S = {หัว, ก้อย}

ตัวอย่างที่ 2 ในการทอดลูกเต๋า 1 ลูก ถ้าเราสนใจแต้ม ของลูกเต๋าที่หงายขึ้น
ผลลัพธ์ที่อาจจะเกิดขึ้นได้คือ ลูกเต๋าขึ้นแต้ม 1 หรือ 2 หรือ 3 หรือ 4 หรือ 5 หรือ 6
ดังนั้นแซมเปิลสเปซที่ได้คือS = {1, 2,3,4,5,6}

ตัวอย่างที่ 3 จากการทดลองสุ่มโดยการทดลองทอดลูกเต๋า 2 ลูก
1. จงหาแซมเปิลสเปซของแต้มของลูกเต๋าที่หงายขึ้น
2. จงหาแซมเปิลสเปซของผลรวมของแต้มบนลูกเต๋า

วิธีทำ    1. เนื่องจากโจทย์สนใจแต้มของลูกเต๋าที่หงายขึ้น
                 ดังนั้นเราต้องเขียนแต้มของลูกเต๋าที่มีโอกาสที่จะหงายขึ้นมาทั้งหมด
                 และเพื่อความสะดวกให้ (a,b) แทนผลลัพธ์ที่อาจจะเกิดขึ้น โดยที่

                         a    แทนแต้มที่หงายขึ้นของลูกเต๋าลูกแรก
                         b    แทนแต้มที่หงายขึ้นของลูกเต๋าลูกที่สอง
                ดังนั้นแซมเปิลสเปซของการทดลองสุ่มคือ
                S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
                       (2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
                       (3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
                       (4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
                       (5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
                       (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

                    2. เนื่องจากโจทย์สนใจผลรวมของแต้มบนลูกเต๋า
                         ดังนั้นเราต้องเขียนผลรวมของแต้มบนลูกเต๋าที่มีโอกาสเกิดขึ้นได้ทั้งหมด
                        จะได้แซมเปิลสเปซของผลรวมของแต้มบนลูกเต๋าทั้ง 2 ลูก คือ {2,3,4,5,6,7,8,9,10,11,12}

ตัวอย่างที่ 4   ในกล่องใบหนึ่งมีลูกบอลสีแดง 2 ลูก สีขาว 1 ลูก ถ้าเราหยิบลูกบอลออกจากกล่องมา 1 ลูก โดยวิธีสุ่ม
                      1. จงหาแซมเปิลสเปซของสีของลูกบอลที่จะเกิดขึ้น
                      2. จงหาแซมเปิลสเปซของลูกบอลที่หยิบออกมาได้

วิธีทำ       1. เนื่องจากโจทย์สนใจสีของลูกบอลที่จะหยิบมาได้
                     ดังนั้นแซมเปิลสเปซของสีของลูกบอลที่หยิบได้คือ S= {สีแดง,สีขาว}
                2. เนื่องจากโจทย์สนใจลูกบอลที่จะหยิบมาได้ ซึ่งมีทั้งหมด 3 ลูก
                     สมมติให้เป็น แดง1 แดง2 ขาว1

ดังนั้นแซมเปลิสเปซของลูกบอลที่หยิบออกมาคือ S = {แดง1,แดง2, ขาว1}

เหตุการณ์ ( Event ) คือ เซตย่อยหรือสับเซต ( Subset ) ของแซมเปิลสเปส ( Sample Space ) เขียนแทนด้วยสัญลักษณ์ E

ตัวอย่างที่ 5 ในการทอดลูกเต๋า 1 ลูก จำนวน 1 ครั้ง และสนใจผลลัพธ์คือแต้มที่จะเกิดขึ้นจงหา

1. แซมเปิลสเปส S

2. เหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลงตัว ( E₂ )
3. เหตุการณ์ที่ได้แต้มคี่ ( E₂ )

วิธีทำ

1. S = {1,2,3,4,5,6 }

2. E₁ = {4,6}

3. E₃ = {1,2,3}

ตัวอย่างที่ 6 ในการสอบวิชาคณิตศาสตร์ของนักศึกษากลุ่มหนึ่ง ซึ่งได้คะแนนสูงสุดเท่ากับ 50 คะแนนต่ำสุด 20คะแนน

1. แซมเปิลสเปส (S) คือ { 20 < X < 50} เมื่อ X เป็นค่าหนึ่ง ๆ
2. เหตุการณ์ที่นักศึกษาได้น้อยกว่า 30

E₁ = { 20 < X < 30}

3. เหตุการณ์ที่นักศึกษาได้คะแนนสูงกว่า 40

E₂ = {40 < X < 50}

การทดลองสุ่ม คือ การทดลองซึ่งทราบผลลัพธ์ที่จะเกิดขึ้นว่าจะเป็นอะไรบ้าง แต่ไม่สามารถที่จะทราบผลลัพธ์ที่เกิดขึ้นได้ถูกต้องแน่นอนว่าจะเกิดอะไรขึ้น เนื่องจากในการทดลองแต่ละครั้งอาจเกิดผลลัพธ์( Outcome ) หลายอย่าง เช่น

การโยนเหรียญบาท 1 เหรียญ ขึ้นไปในอากาศ แล้วตกลงพื้นอย่างอิสระ สามารถที่จะทำนายว่าจะออกหัว (Head ) หรือออกก้อย ( Till ) ซึ่งเป็นผลลัพธ์ได้ล่วงหน้า

การโยนลูกเต๋า 1 ลูก ขึ้นไปในอากาศ แล้วตกลงพื้นอย่างอิสระ ซึ่งเราทราบว่าผลลัพธ์ที่จะเกิดขึ้น คือ 1, 2, 3, 4, 5, 6 แต่ว่าผลลัพธ์มีหลายอย่าง เราไม่สามารถทำนายได้ว่าจะออกเลขอะไร

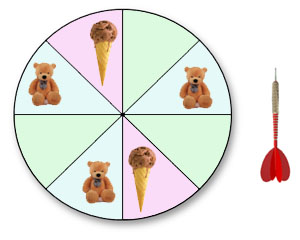
เกมปาเป้ามีรางวัลตามภาพในเป้า เป้าถูกปั่นให้หมุนจนไม่เห็นภาพรางวัล แล้วให้ผู้เล่นเกมปาลูกดอกใส่เป้า 1 ครั้ง ลูกดอกปักในช่องใด ผู้เล่นเกมได้รางวัลตามภาพที่อยู่ในช่องนั้น ถ้าลูกดอกปักในช่องที่ไม่มีภาพ ผู้เล่นเกมไม่ได้รางวัล จงหาความน่าจะเป็นที่
1.1) ผู้เล่นได้รางวัลเป็นตุ๊กตาหมี
1.2) ผู้เล่นได้รางวัลเป็นไอศรีม
1.3) ผู้เล่นไม่ได้รางวัลใดเลย
1.4) ผู้เล่นได้รางวัลใดรางวัลหนึ่ง

.....เฉลย ข้อ 1

ตูนทายวันเกิดเพื่อน โดยเพื่อนบอกใบ้ให้ว่าเขาเกิดเดือนมีนาคม จงหาความน่าจะเป็นที่ตูนทายถูกว่าเพื่อนเกิดวันที่เท่าไร

.....เฉลย ข้อ 2

ในขวดโหล มีลูกกวาดรสส้ม 4 ลูก
ลูกกวาดรสมะนาว 3 ลูก
ลูกกวาดรสสตรอเบอรี่ 5 ลูก
หยิบลูกกวาด 1 ลูกจากขวดโหลนี้
จงหาความน่าจะเป็นที่หยิบได้ลูกกวาดรสมะนาว

.....เฉลย ข้อ 3

ในถุงมีธนบัตรใบละ 1,000 บาท 2 ใบ
ธนบัตรใบละ 500 บาท 3 ใบ
ธนบัตรใบละ 100 บาท 8 ใบ
ธนบัตรใบละ 50 บาท 10 ใบ
ธนบัตรใบละ 20 บาท 15 ใบ
ล้วงธนบัตร 1 ใบจากถุง
จงหาความน่าจะเป็นที่ล้วงได้ธนบัตรที่มีมูลค่าสูงสุด

.....เฉลย ข้อ 4

ลานจอดรถแห่งหนึ่งมีรถจอดอยู่ 100 คัน
เป็นรถเก๋ง 60 คัน
รถกระบะ 30 คัน
ที่เหลือเป็นรถตู้
รถทุกคันมีโอกาสที่จะขับออกจากลาดจอดรถเท่ากัน
จงหาความน่าจะเป็นที่รถคันแรกที่ขับออกจากลานจอดรถเป็นรถตู้

.....เฉลย ข้อ 5

แจกแบบสอบถาม 100 ฉบับ เพื่อสำรวจว่าผู้ชมชอบรายการโทรทัศน์ประเภทใด (ผู้ตอบแบบสอบถามเลือกตอบได้เพียง 1 รายการ) ผลการสำรวจเป็นดังนี้

รายการ	จำนวนผู้ที่ชอบดู
ละคร	60
มิวสิควิดีโอ	20
เกมโชว์	10
ข่าว	5
สารคดี	5
* รวม *	100

สุ่มหยิบแบบสอบถามมา 1 ฉบับ
จงหาความน่าจะเป็นที่ไม่พบคนที่ชอบดูข่าว

.....เฉลย ข้อ 6

งานวิจัยชิ้นหนึ่งเก็บสถิติของผู้ที่เสียชีวิตในช่วงอายุต่าง ๆ กันดังตาราง

เสียชีวิตเมื่ออายุ	จำนวนผู้เสียชีวิต
0 - 10	1
11 - 20	2
21 - 30	8
31 - 40	12
41 - 50	18
51 - 60	20
61 - 70	24
71 - 80	10
81 - 90	3
91 - 100	2

ใช้สถิติจากงานวิจัยนี้คำนวณความน่าจะเป็นที่นายยั่งยืนจะเสียชีวิตเมื่ออายุ 80 ปี

.....เฉลย ข้อ 7

โยนลูกเต๋า 1 ลูก 1 ครั้ง
จงหาความน่าจะเป็นที่ได้แต้มที่หารด้วย 3 ลงตัว

.....เฉลย ข้อ 8

นักเรียนห้องหนึ่งประกอบด้วยนักเรียนชาย 20 คน นักเรียนหญิง 25 คน
นักเรียนห้องนี้มีผู้ที่เป็นจิตอาสา 18 คน ซึ่งเป็นชาย 8 คนและเป็นหญิง 10 คน
ในการแจกของขวัญวันเด็ก
นักเรียนหญิงได้รับโบว์ผูกผม
นักเรียนชายได้รับหมวกแก็ป
นักเรียนที่เป็นจิตอาสาได้รับเสื้อยืด
จงหาความน่าจะเป็นที่นักเรียนห้องนี้ได้รับทั้งโบว์ผูกผมและเสื้อยืด

.....เฉลย ข้อ 9

10)

รายการเกมโชว์รายการหนึ่ง มีแผ่นป้าย 30 แผ่น เขียนเลขกำกับไว้ตั้งแต่ 1 ถึง 30 ผู้ที่เล่นเกมจนเข้ารอบสุดท้ายได้รางวัลโดยให้เลือกแผ่นป้าย 1 แผ่น จากแผ่นป้ายทั้งหมด 30 แผ่น

ถ้าเลือกได้เลขที่หารด้วย 2 ลงตัวจะได้รางวัลเป็นโทรศัพท์มือถือ
ถ้าเลือกได้เลขที่หารด้วย 3 ลงตัวจะได้รางวัลเป็นโทรทัศน์
แป๋วเข้ารอบสุดท้าย จงหาความน่าจะเป็นที่แป๋วได้ทั้งโทรศัพท์มือถือและโทรทัศน์

.....เฉลย ข้อ 10

ตัวอย่างที่ 1 มีเสื้อ 3 ตัว กางเกง 4 ตัว จะจัดเป็นชุดที่ไม่ซ้ำกันได้กี่แบบ …….ตอบ… $3\times 4 = 12$ แบบ
……………มีเรือวิ่งข้ามฟาก 3 ลำ จะนั่งเรือไปและกลับไม่ให้ซ้ำลำกันได้กี่วิธี …….ตอบ… $3\times 2 = 6$ วิธี
……………ทอดลูกเต๋า 2 ครั้ง จะมีผลออกมาได้กี่แบบ ……. ตอบ… $6\times 6 = 36$ แบบ

ตัวอย่างที่ 2 ใช้ตัวเลข 0, 1, 2, 3, 4 และ 5 มาสร้างจำนวน 3 หลัก จะสร้างได้กี่จำนวน ถ้ากำหนดให้
…..1) แต่ละหลักไม่ซ้ำกัน …….ตอบ… $5\times 5\times 4 = 100$ จำนวน
…..2) เป็นจำนวนคี่และแต่ละหลักไม่ซ้ำกัน …….ตอบ… $4\times 4\times 3 = 48$ จำนวน
…..3) มีค่ามากกว่า 350 และแต่ละหลักไม่ซ้ำกัน……. ตอบ… $\left ( 1\times 1\times 3 \right )+\left ( 2\times 5\times 4 \right ) = 43$ จำนวน
…..4) หารด้วย 10 ลงตัว……. ตอบ… $1\times 5\times 6 = 30$ จำนวน

ตัวอย่างที่ 3 บริษัทรถยนต์แห่งหนึ่งตัวถังรถยนต์ออกมา 2 แบบ มีเครื่องยนต์ 2 ขนาด และสีต่าง ๆ กัน 3 สี ถ้าต้องการแสดงรถยนต์ให้ครบทุกแบบ ทุกขนาดและทุกสี จะต้องใช้รถยนต์อย่างน้อยที่สุดกี่คัน
….วิธีทำ เลือกตัวถังแล้วเลือกเครื่องยนต์แล้วเลือกสีได้ $2\times 2\times 3 = 12$ คัน

ตัวอย่างที่ 4 จัดคน 10 คน นั่งเก้าอี้ 3 ตัว ซึ่งวางเรียงเป็นแถวเดียวกันได้ทั้งหมดกี่วิธี
….วิธีทำ จัดคนเข้านั่งได้ $10\times 9\times 8 = 720$ วิธี

ตัวอย่างที่ 5 ข้อสอบฉบับหนึ่งมี 10 ข้อเป็นแบบถูก – ผิด จะมีวิธีตอบข้อสอบที่ไม่ซ้ำกันเลยได้ทั้งหมดกี่วิธี
….วิธีทำ…..ทำแบบทดสอบได้ $2\times 2\times 2 \times \cdots \times 2 = 2^{10} = 1024$ วิธี

ตัวอย่างที่ 6 ในการเลือกตั้งคณะกรรมการชุดหนึ่งจะประกอบไปด้วย ประธาน รองประธาน เหรัญญิก และเลขานุการ โดยที่กรรมการแต่ละคนจะดำรงตำแหน่งได้เพียงตำแหน่งเดียวเท่านั้น ถ้ามีผู้สมัครทั้งหมด 6 คน เป็นชาย 2 คน เป็นหญิง 4 คน ผลการเลือกตั้งกรรมการชุดนี้จะมีได้ทั้งหมดกี่แบบที่ต่างกัน โดยที่
……. 1. ไม่มีเงื่อนไขเพิ่มเติม …….ตอบ… $6\times 5\times 4\times 3 = 360$ แบบ
……. 2. กำหนดให้ประธานเป็นชาย และเลขาต้องเป็นหญิง …….ตอบ… $2\times 4\times 4\times 3 = 96$ แบบ
……. 3. กรรมการต้องเป็นหญิงล้วน …….ตอบ… $4\times 3\times 2\times 1 = 24$ แบบ

ตัวอย่างที่ 7 หมายเลขโทรศัพท์เคลื่อนที่ที่ขึ้นต้นด้วย 086720 xxxx จะมีทั้งหมดกี่หมายเลข
….วิธีทำ…..เลือกหมายเลขขึ้นต้นได้ 1 วิธีจากนั้นเลือกอีก 4 หมายเลขที่เหลือได้ จะได้ $1\times 10\times 10\times 10\times 10 = 10,000$ หมายเลข

ตัวอย่างที่ 8 จากอักษรในคำว่า “PHYSIC” นำมาสร้างคำใหม่ประกอบด้วย 3 อักษร ต่างกัน (ไม่สนใจความหมายของคำเหล่านั้น) โดยที่
……. 1. ไม่มีเงื่อนไขเพิ่มเติม …….ตอบ… $6\times 5\times 4 = 120$ วิธี
……. 2. ต้องเป็นพยัญชนะทั้งหมด …….ตอบ… $5\times 4\times 3 = 60$ วิธี

ตัวอย่างที่ 9 ห้องประชุมแห่งหนึ่งมี 3 ประตู จงหาวิธีในการเดินเข้า – ออกห้องประชุม โดยมีเงื่อนไขต่างกัน ดังนี้
……. 1. จำนวนวิธีในการเดินเข้า …….ตอบ… $3$ วิธี
……. 2. จำนวนวิธีในการเดินเข้า – ออก …….ตอบ… $3\times 3 = 9$ วิธี
……. 3. จำนวนวิธีในการเดินเข้า – ออก โดยไม่ซ้ำประตูกัน …….ตอบ… $3\times 2 = 6$ วิธี
……. 4. จำนวนวิธีในการเดินเข้า – ออก โดยใช้ประตูเดิม …….ตอบ… $3\times 1 = 3$ วิธี

ตัวอย่างที่ 10 จดหมายแตกต่างกัน 3 ฉบับ ต้องการทิ้งจดหมายในตู้ไปรษณีย์ 4 ตู้ จะทิ้งได้กี่วิธี โดยที่
……. 1. ไม่มีเงื่อนไขเพิ่มเติม …….ตอบ… $4\times 4\times 4 = 64$ วิธี
……. 2. ห้ามทิ้งซ้ำตู้กัน …….ตอบ… $4\times 3\times 2 = 24$ วิธี

วิชา คณิตศาสตร์

หน้าเว็บ

บทที่2

ไม่มีความคิดเห็น:

แสดงความคิดเห็น